Quantum Computation with Superconducting Qubits
- Continuous qubit trajectories
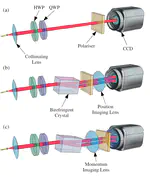
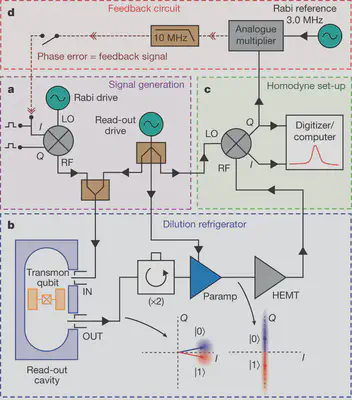
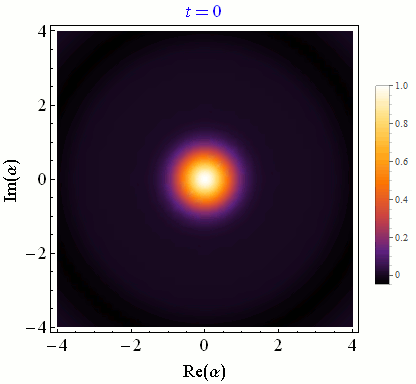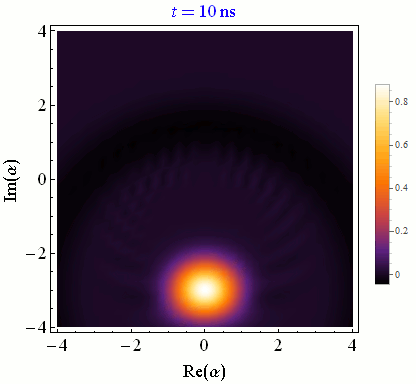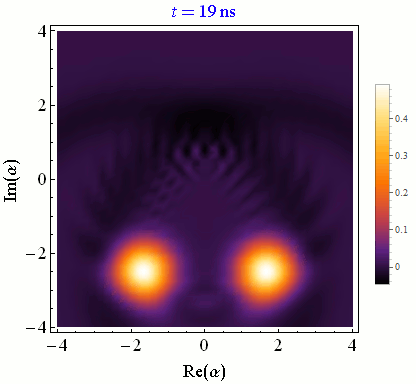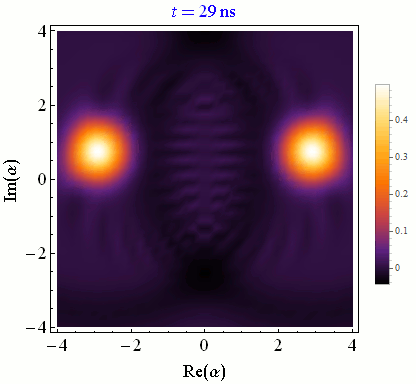
In circuit QED we infer the state of a quantum bit (qubit) by making a quadrature measurement on an interacting microwave resonator field. Achieving high-fidelity state-tracking from the collected noisy quadrature signal is a necessary prerequisite for more sophisticated quantum information tasks.
 |  |
|---|
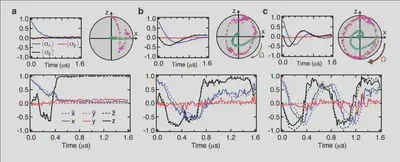
Quantum feedback and control
One can continuously monitor partial information about a quantum system in order to control experimental parameters in real time for a variety of purposes, such as state purification and initialization, coherence stabilization, and error correction.Correlated multi-qubit measurement
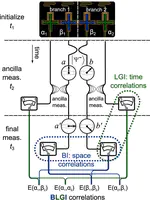
The expected advantages of quantum computing are rooted in multi-qubit coherence and entanglement effects, with information extracted through uncorrelated high-fidelity projective measurements. A less-explored possibility is exploiting the spatio-temporal correlations between generalized (e.g. weaker) measurements to extract useful information.Quantum Parameter Estimation
Determining how well one is modeling the physical system in the lab is not a trivial matter. Modern tomographic methods under development use compressive sensing and adaptive estimation techniques to reduce the amount of data that one needs to collect, and reduce the computational resources required to reconstruct the estimates.Machine Learning for Device Characterization
As chips become more complex in the laboratory, calibration and tune-up becomes an increasingly daunting task. Modern machine learning methods offer novel solutions for auto-calibrating device parameters and tracking dynamics occuring during a computational run.
Quantum Information and Measurement Theory
Quantum instruments
Measurements are a dynamical process in quantum mechanics, best represented as a collection of transformations that are in one-to-one correspondence with the distinguishable results of a physical detector. The information collected by the detector updates the quantum state according to these transformations, which generalize Bayes’ rule from classical probability theory. Unlike textbook quantum measurements, the quantum state only partially “collapses” when partial information is collected.Weak Measurements
When almost no information is gathered by a detector making a measurement, the quantum state is almost entirely preserved. Nevertheless, taking a sufficiently large sample of data still permits the same average infomation to be extracted as textbook projective measurements that fully collapses the state.Quantum trajectories
Discretizing time into small pieces and applying both natural state evolution and measurement-induced state updates at each time step yields a quantum trajectory. Generally these state trajectories show a competition between the natural evolution from the Schroedinger equation and the stochastic evolution from the measurement itself. Stronger measurements per unit time rapidly collapse the state and pin it near the measurement eigenstates, between which quantum jumps can then be tracked. Weaker measurements per unit time minimally perturb the natural evolution, allowing temporal correlations of this coherent evolution to be faithfully extracted.Conditioned Statistics
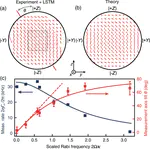
Many strange features of quantum mechanics only manifest when several measurements are correlated. Examples include quantum erasure, violations of local realism via Bell inequalities, violations of macrorealism via Leggett-Garg inequalities, anomalously large conditioned averages (including weak values), and even the bunching and anti-bunching behavior of particle statistics.
Foundations of Physics
Quantum Weak Values
Averaging weak measurements of a pre- and post-selected ensemble consistently produces an average described by a curious quantity known as a weak value, rather than the usual expectation value. These quantities appear througohut the quantum formalism in surprising ways and are closely related to quasiprobabilistic descriptions of joint observable statistics.Contextuality, Locality, and Macrorealism
While most agree that quantum mechanics is weird, it is more difficult to quantify that weirdness in a satisfying (and experimentally accessible) way. The arguably most successful efforts have isolated specific axioms that are aligned with our macroscopic intuition of the physical world (e.g., noncontextual value assignment, locality, and realism), and have constructed rigorous tests to show exactly where quantum mechanics violates these seemingly safe assumptions.Noncommutative Probability Theory
The infamous “state collapse” in the quantum theory can be understood as a straightforward generalization of Bayes’ theorem in classical probability theory. This observation places probability distributions and quantum states on analogous footing, making the study of noncommutative probability theory a promising route toward reformulating the quantum theory.Applications of Clifford Algebras
Through an accident of historical development, the practical application of Clifford algebras has been left largely undeveloped in favor of less expressive mathematical formalisms (e.g., the vector calculus of Gibbs/Heaviside). More careful scrutiny reveals that Clifford algebras greatly simplify the mathematical expression of physical law in highly suggestive ways. One example is the unification of Maxwell’s equations into a single equation: ∇F = j, where F = E+BI is the proper (frame-independent) generalization of the Riemann-Silberstein complex electromagnetic field vector, j is the 4-vector current density, ∇ is the same Dirac differential operator as for the relativistic quantum electron, and I is the intrinsic pseudoscalar (volume element) of spacetime.Relativistic Fields
Even before introducing second quantization, relativistic fields have remarkably rich structure that is important for practical applications. Notably, modern experimental research in classical optics has forced the reinvestigation of troublesome topics, such as the local momentum of optical vortex singularities, and the proper theoretical separation of orbital and spin parts of the angular momentum density (which can be separately measured with probe particles).
Funding Sources
PI: Dr. Irfan Siddiqi, University of California, Berkeley
Co-PI: Dr. Justin Dressel, Chapman University
Co-PI: Dr. Andrew N. Jordan, University of Rochester / Chapman University
Subcontract amount: $783,867
Award end date: Sep. 2026
PI: Dr. Justin Dressel, Chapman University
BSF Collaborator: Dr. Lev Vaidman, University of Tel Aviv, Israel
Award amount: $321,000
PI: Dr. Irfan Siddiqi, University of California, Berkeley
Co-PI: Dr. Justin Dressel, Chapman University
Co-PI: Dr. Andrew N. Jordan, University of Rochester / Chapman University
Co-PI: Dr. Joseph Emerson, University of Waterloo
Subcontract amount: $546,328
PI: Dr. Irfan Siddqi, University of California, Berkeley
Co-PI: Dr. Justin Dressel, Chapman University
Co-PI: Dr. Andrew N. Jordan, University of Rochester
Co-PI: Dr. Alexander N. Korotkov, University of California, Riverside
Subcontract amount: $300,000